It’s been quite a while since I wrote my last blog article and so this seems to be a nice and perfect time to write something. Though I am not a very big fan of maths and for some reason I have always found it super challenging but today I am going to be writing on something relevant to the subject field. No worries if you are not a maths enthusiast but if you happen to have even the slightest of interest in philosophy and history you will find this piece of writing quite interesting.
It’s unfortunate that I did not get the chance to study Philosophy earlier despite having deep interest in the subject but here I am studying a philosophy course called “Logic-how to think” from an Ex-formanite who is also a PhD in Philosophy from University of Edinburgh. I believe that all great Philosophers like Socrates, Aristotle, Pythagoras etc were great thinkers and were alike in a way that they had deep craving to understand the meaning of life. Either it be the understanding of virtue, politics or ethics (Socrates) or it be the study of logic or metaphysics ( Aristotle), or the understanding of geometry and medicine (Pythagoras) all these great thinkers wanted to know more about life and their existence. They were the kind of people who would think of things beyond obvious and beyond the monotonous life of their times.

Now one of the reasons for which I am taking Logic this semester is because it gives great promise for it provides a mastery of invention and judgment, as well as supplies ability to divide, define, and prove with conviction. It is such an important part of philosophy that it serves the other parts in much the same way as the soul does the body. However, I will be talking more about it once I have more knowledge regarding it. And so for now I will stick to the topic which is “Pythagoras-the pioneer of Pythagoras theorem”.
As astonishing as it may sound Pythagoras did not leave a single written work behind him. However, Heraclitus the natural scientist pretty well shouts it out when he says: “Pythagoras, son of Mnesarchus , practiced inquiry more than any other man, and selecting from the writing of those before him he made a wisdom of his own – a polymath, a worthless artifice”. (Pythagoras by Kitty Ferguson)

Pythagoras believed that all things revolve around numbers and this discovery was made by him in music. The first natural law ever formulated mathematically was the relationship between musical pitch and the length of a vibrating harp string and Pythagoras was the one to formulate it. He also believed that the universe itself hummed with its own harmony—beautiful, divine, and inaudible to human ears. He characterized the intervals between successive orbits, such as those of Mercury and Venus, as either tones or half-tones (the smallest intervals in the musical scale), adding up to seven whole tones that form a perfectly harmonious natural order. According to many ancient sources Pythagoras applied his discoveries in music theory to the behavior of the celestial objects. Pluck a string, and the pitch of the note it produces is related to the length of the string. When the lengths of two strings are a simple ratio—1/2, 2/3, and so on—the notes together sound harmonious.
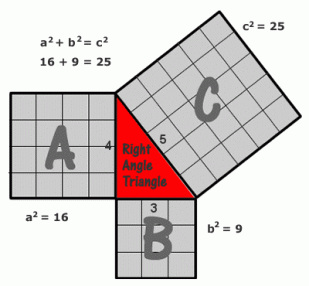
Apart from this, he also proposed the mathematical concept known as “The Pythagoras Theorem” which we are all very familiar with. Pythagoras’ Theorem and the properties of right-angled triangles seems to be the most ancient and widespread mathematical development after basic arithmetic and geometry, and it was touched on in some of the most ancient mathematical texts from Babylon and Egypt, dating from over a thousand years earlier. He deduced that, for any right-angled triangle, the square of the length of the hypotenuse (the longest side, opposite the right angle) is equal to the sum of the square of the other two sides (or “legs”). Written as an equation: a2 + b2 = c2. The simplest and most commonly quoted example of a Pythagorean triangle is one with sides of 3, 4 and 5 units (32 + 42 = 52, as can be seen by drawing a grid of unit squares on each side as in the diagram given below), but there are a potentially infinite number of other integer “Pythagorean triples”, starting with (5, 12 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41), etc. It should be noted, however that (6, 8, 10) is not what is known as a “primitive” Pythagorean triple, because it is just a multiple of (3, 4, 5).
Among his other major achievements in geometry, Pythagoras also realized that the sum of the angles of a triangle is equal to two right angles (180°), and probably also the generalization which states that the sum of the interior angles of a polygon with n sides is equal to (2n – 4) right angles, and that the sum of its exterior angles equals 4 right angles. They were able to construct figures of a given area, and to use simple geometrical algebra, for example to solve equations such as a(a – x) = x2 by geometrical means.
To conclude, Pythagoras made some thought provoking discoveries which are studied and practiced even to this day. His calm nature and passion for wisdom was what helped him in creating breakthroughs in the fields of maths, science and philosophy.
